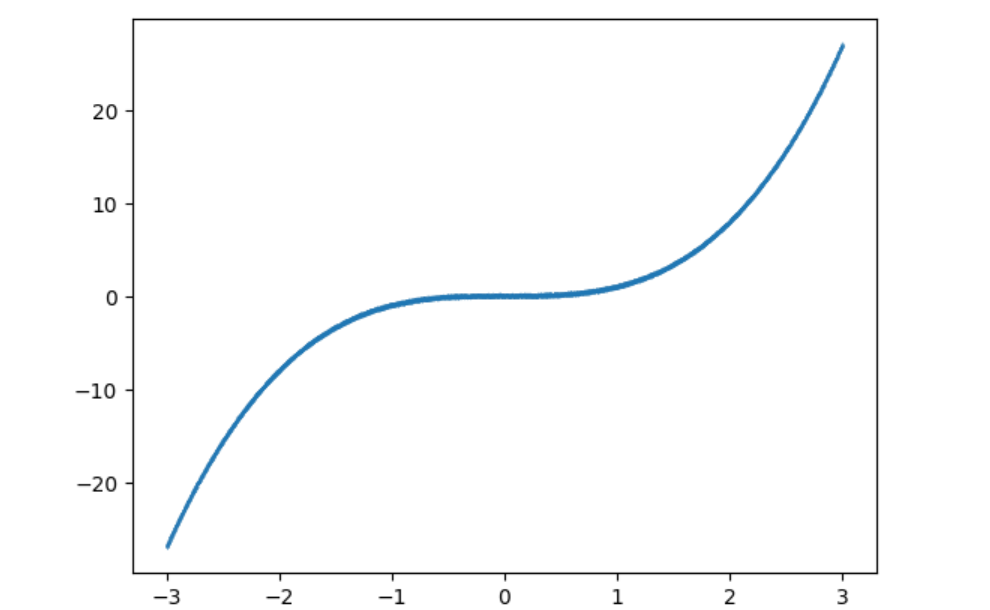
用Python 程序根据一元三次方程自动生成一批数据样本
# 根据一元三次方程自动生成一批数据样本
import torch
import matplotlib.pyplot as plt
x = torch.unsqueeze(torch.linspace(-3, 3, 10000), dim = 1)
y = x.pow(3) + 0.3 * torch.rand(x.size())
plt.scatter(x.numpy(), y.numpy(), s=0.01)
plt.show()
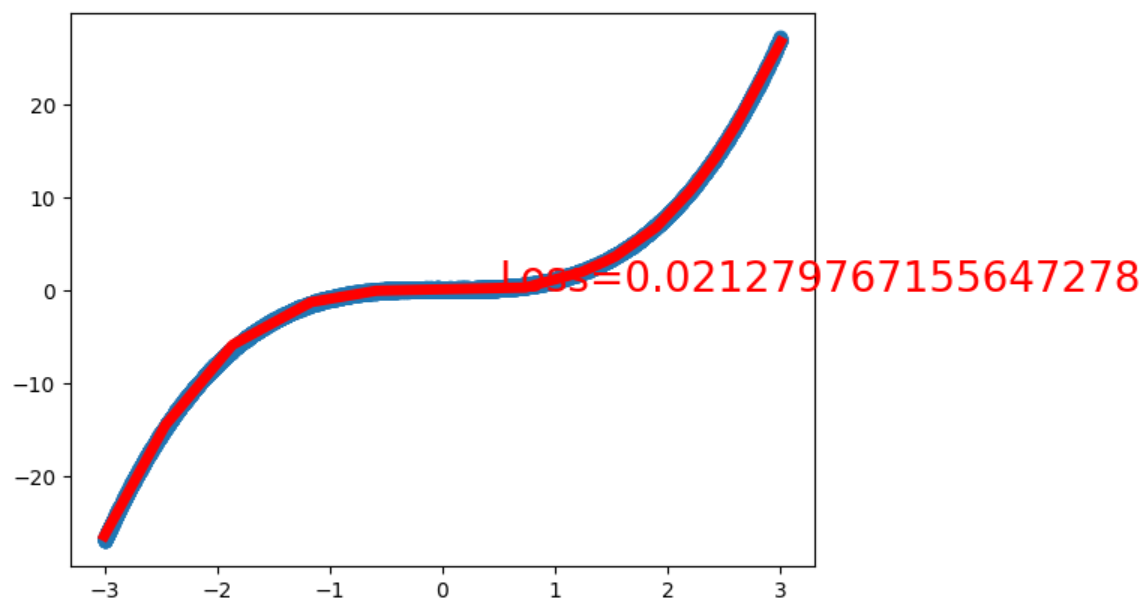
编写神经网络,以及进行训练
# 绘图函数
def draw(output, loss):
plt.cla()
plt.scatter(x.numpy(), y.numpy())
plt.plot(x.numpy(), output.data.numpy(), 'r-', lw=5)
plt.text(0.5, 0, 'Loss=%s' % (loss.item()), fontdict={'size':20, 'color':'red'})
plt.pause(0.005)
# 设计神经网络模型,一个输入层,一个隐藏层,一个输出层
from torch import nn, optim
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self, input_feature, num_hidden, outputs):
super(Net, self).__init__()
self.hidden = nn.Linear(input_feature, num_hidden)
self.out = nn.Linear(num_hidden, outputs)
def forward(self, x):
x = F.relu(self.hidden(x))
x = self.out(x)
return x
# 输入为1维,隐藏层节点数为20,输出为1维
net = Net(input_feature=1, num_hidden=20, outputs=1)
inputs = x
target = y
# 将优化器设置为随机梯度下降,损失函数设为均方误差
optimizer = optim.SGD(net.parameters(), lr=0.01)
criterion = nn.MSELoss()
# 训练函数
def train(model, criterion, optimizer, epochs):
for epoch in range(epochs):
output = model(inputs)
loss = criterion(output, target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 80 == 0:
draw(output, loss)
return model, loss
# 训练10000次,并打印最终的损失值
net, loss = train(net, criterion, optimizer, 10000)
print("final loss:", loss.item())
层层拟合,最终的结果如下